Estadística: se considera que es un conjunto de técnicas, que tienen el propósito de describir fenómenos; que se manifiestan a través de datos que presentan variabilidad.

También es una herramienta poderosa que se utiliza para analizar datos, y sacar conclusiones significativas de ellos. Las medidas de tendencia central son medidas estadísticas que pretenden resumir en un solo valor a un conjunto de valores. Representan un centro en torno al cual se encuentra ubicado el conjunto de los datos. Las medidas de tendencia central más utilizadas son: media, mediana y moda. Por lo tanto, existen dos ramas principales de la estadística: la estadística descriptiva y la estadística inferencial. Cada una de ellas son importantes y útiles, pero tienen diferentes objetivos y enfoques.

La estadística descriptiva, se enfoca en resumir y describir datos que ya tenemos, en esta rama se emplea técnicas de tendencia central, (media, mediana y moda)

Media: es la media aritmética en un conjunto de valores numéricos. Es el valor promedio en un conjunto de datos. Y esta la calculamos, sumando todos los valores y dividirlos por la cantidad de datos.

A continuación, presentamos la formula y una representación.

En esta cuestión de vemos de afirmar que, para poder aplicar la formula, se debe catalogar bien de acuerdo a nuestros tipos de datos, o de la forma que se quiera trabajar si queremos obtener un dato de un grupo de población o de dicha población obtener una muestra.

Mediana: es el valor que ocupa el lugar central, de todos los datos; cuando estos están ordenados de menor a mayor.

Mediana se representa Me. Considerando que esta solo se puede hallar solo para variables cuantitativas.

Ejemplo de cálculo simple de la mediana

1.- ordenamos los datos de menor a mayor.

2.- si la serie tiene un numero impar, de medidas la mediana es la puntuación central de la misma.

Ejemplo:

2,3,4,4,5,5,5,6,6.

Me=5

3.- si la serie tiene un numero par de puntuaciones la mediana es la media entre las dos puntuaciones centrales.

Ejemplo:

7,8,9,10,11,12.

Me= 9+10/2= 9.5

Hacemos el conteo uno y uno, de los datos obtenidos, y en este caso, como al medio tenemos dos números, lo que hacemos es sumar esos números y dividirlos entre 2, posteriormente obtenemos nuestra puntuación central.

Formula de la mediana

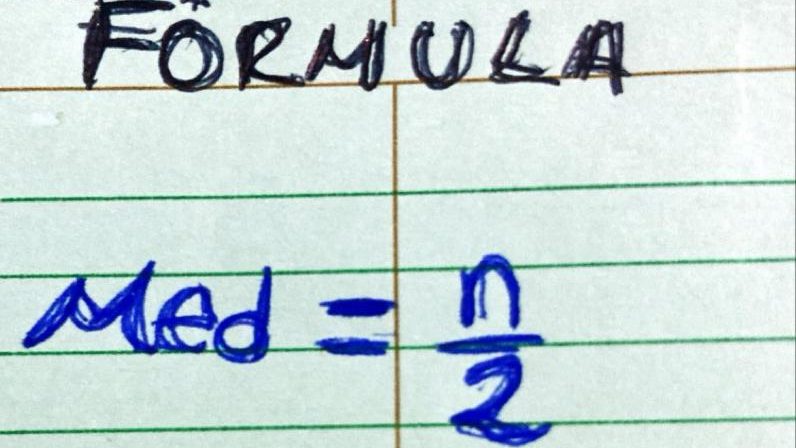
Moda: La moda de una distribución se define como el valor de la variable que más se repite. En un polígono de frecuencia la moda corresponde al valor de la variable que está bajo el punto más alto del gráfico. Una muestra puede tener más de una moda.

En un conjunto de datos, puede haber más de una moda. Un conjunto con dos modas es bimodal, un conjunto con tres modas es trimodal, etc. También puede haber un conjunto de datos sin moda.

Ejemplo 1: busque la moda del conjunto

3,4,5,5,6,7,7,7,8,9.

En el conjunto de datos, los números 3, 4, 6, 8 y 9 se repiten una vez cada uno.

El número 5 se repite dos veces y el 7 se repite tres veces.

Así, la moda del conjunto de datos es 7.

Ejemplo2: busque la moda del conjunto

{15, 18, 20, 20, 24, 26, 28, 30, 40, 55, 55}

En el conjunto de datos, los números 15, 18, 24, 26, 28, 30 y 40 se repiten una vez cada uno.

Los números 20 y 55 se repiten dos veces.

En este caso, el conjunto de datos tiene dos modas, así este es bimodal.

Las modas son 20 y 55.

La moda puede ser usada como una medida de tendencia central de un conjunto de datos.

Seguimos con la estadística descriptiva, y con base a eso tenemos mas medidas de dispersión (varianza y desviación estándar) y gráficos (histogramas, diagramas de caja y bigotes, entre otros) para resumir y visualizar los datos. El objetivo principal de la estadística descriptiva es hacer que los datos sean más fáciles de entender y comunicar, y para ello se utilizan técnicas de análisis de datos simples.

Rango de variación: Se define como la diferencia entre el mayor valor de la variable y el menor valor de la variable.

RANGO DE VARIACION= MAX-MIN

La mejor medida de dispersión, y la más generalizada es la varianza, o su raíz cuadrada, la desviación estándar. La varianza se representa con el símbolo σ² (sigma cuadrado) para el universo o población y con el símbolo s2 (s cuadrado), cuando se trata de la muestra. La desviación estándar, que es la raíz cuadrada de la varianza, se representa por σ (sigma) cuando pertenece al universo o población y por “s”, cuando pertenece a la muestra. σ² y σ son parámetros, constantes para una población particular; s2 y s son estadígrafos, valores que cambian de muestra en muestra dentro de una misma población. La varianza se expresa en unidades de variable al cuadrado y la desviación estándar simplemente en unidades de variable.

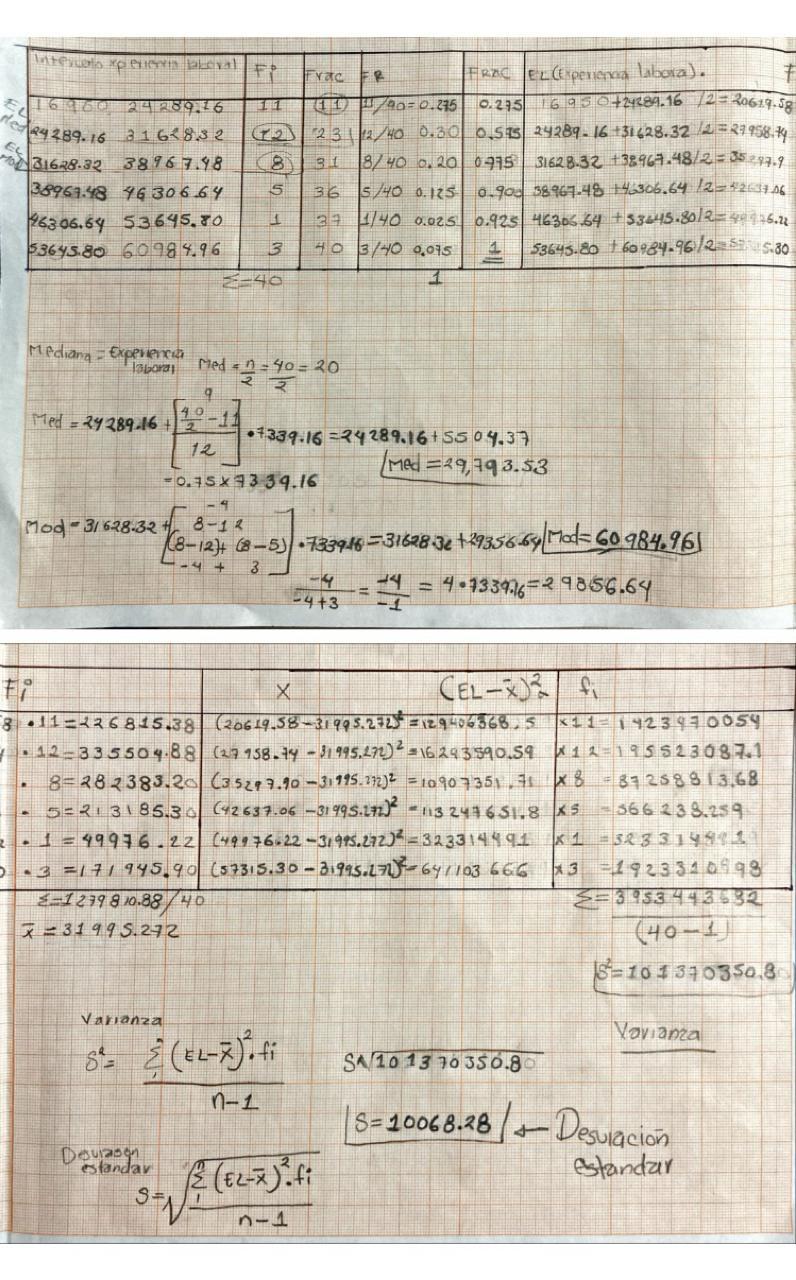
A CONTINUACION SE MUESTRA UN EJEMPLO DE LO YA MENCIONADO, DE COMO PODEMOS EXPRESAR LA BASE DE DATOS POR MEDIO DE LA SIGUIENTE TABLA.

ACT.1-LA BASE DE DATOS SE CONFORMO CON LA INFORMACION SUMINISTRADA POR LA ENTIDAD FINANCIERA BANK AMERICA CON BASE A LA TABLA REALIZA LO SIGUIENTE:

 

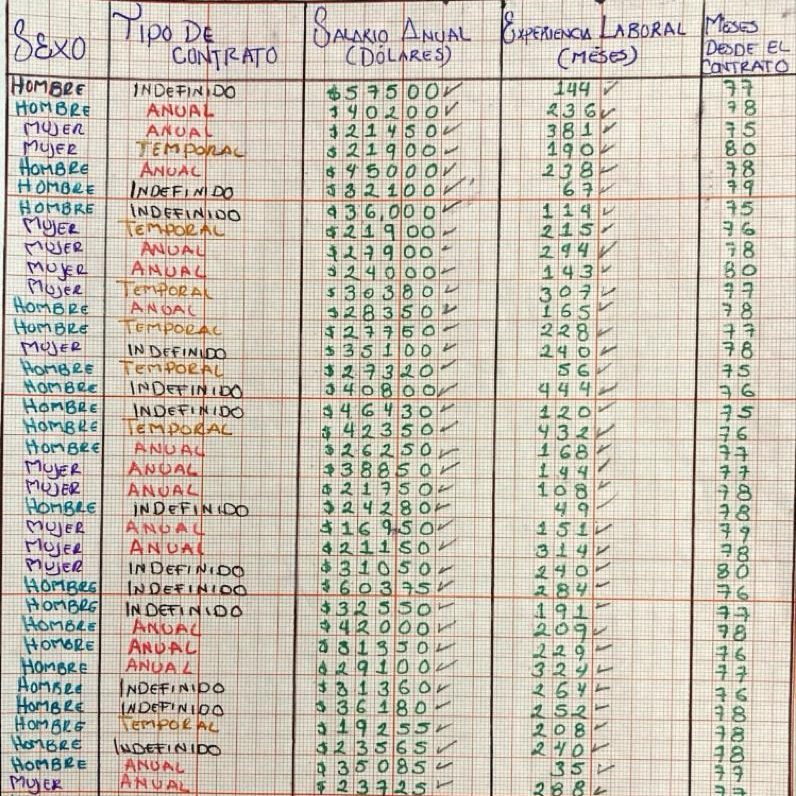
1. Clasifica cada variable en cualitativa o cuantitativa (discreta o continua)

Como ya sabemos dentro de la estadística existen 2 tipos de variables:

• Cualitativa: estas no son representados con valores numéricos, lo cual conlleva a dividirse en nominal: esta no tiene un cierto orden, ni jerarquía, tales como; sexo, lugares, estado civil. Y existe la forma ordinal: estas si son organizadas de acuerdo a su clasificación.
• Cuantitativa: esta a diferencia de la cualitativa, sus resultados son numéricos y se divide en: Discreta: que es expresada con valores enteros y continua: que puede tomar cualquier valor dentro de un intervalo, con números en decimal.

De acuerdo a la tabla las variaciones son las siguientes.

• Sexo: cualitativa (nominal)
• Tipo de contrato: cualitativa (ordinal)
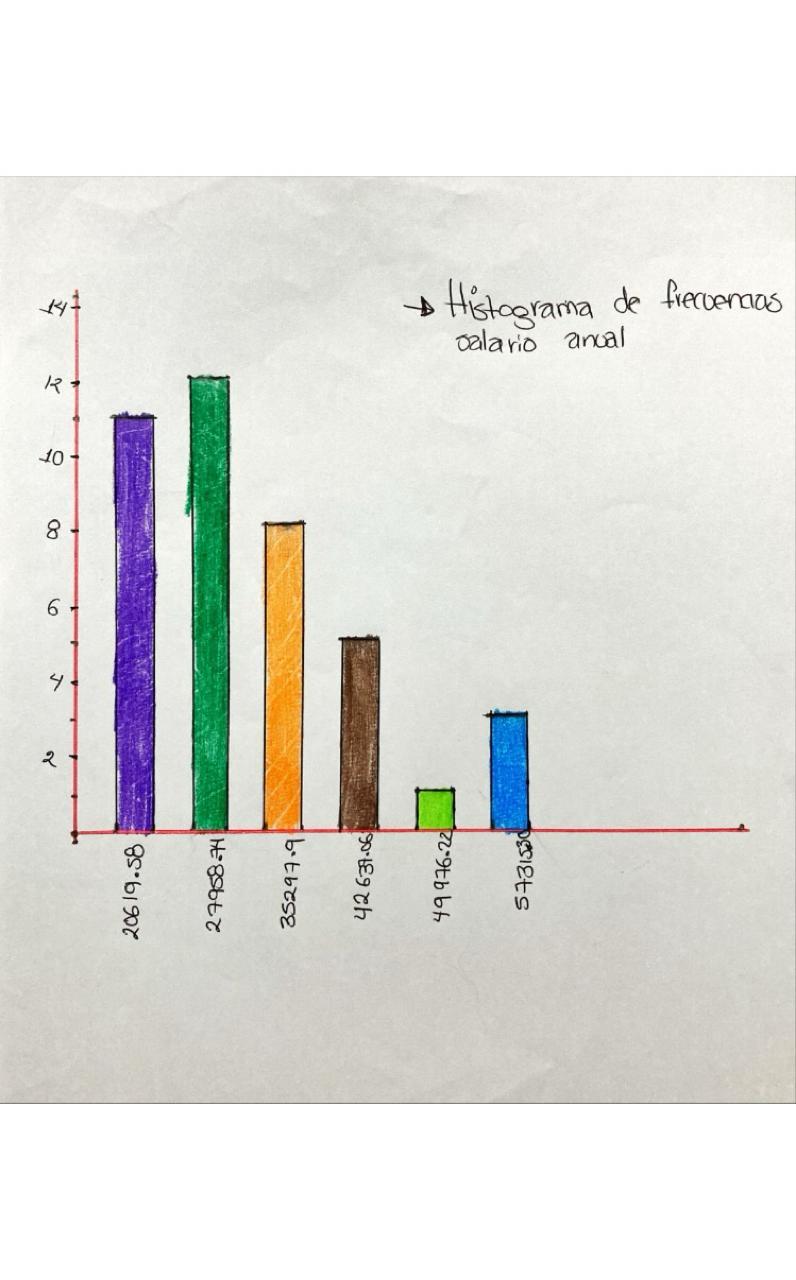
• Salario anual (dólares): cuantitativa (continua)
• Experiencia laboral (meses): cuantitativa (discreta)
• Meses desde el contrato: cuantitativa (discreta)

1. Elabora una distribución de frecuencias absolutas y relativas para los datos agrupados de la variable salario anual y represéntala en la gráfica correspondiente.

• Determina la media aritmética la moda y la mediana para los datos de la variable salario anual selecciona una de ellas para que represente al conjunto y explícala.

Estadística inferencial es una herramienta, en la toma de decisiones basado en datos.

• Escribe una conclusión sobre la distribución de datos.

La distribución de los datos es precisa, si estos los organizamos en orden, posteriormente estos nos brindaran una información más clara y más rápida de entender.

Nos damos cuenta que es necesario tener la información más precisa posible, para poder tomar decisiones importantes y oportunas y la distribución de datos nos brinda lo necesario.

• Elabora una distribución de frecuencias relativas de la variable tipo contrato y represéntalas en la gráfica pertinente.

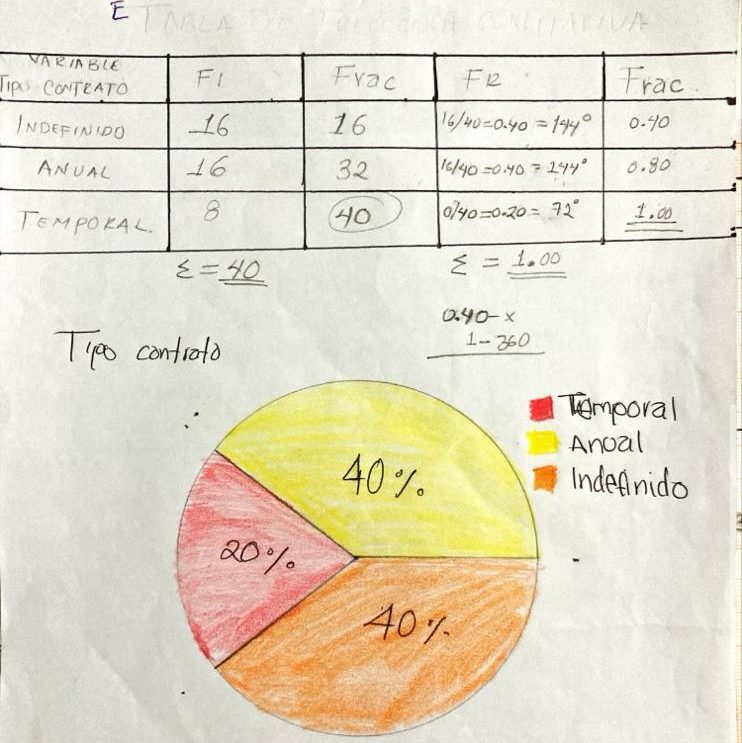
• Obtén la medida de tendencia central correspondiente a este tipo de variable y al respecto escribe una conclusión.

De acuerdo a los datos enmarcados en la tabla recordemos que la moda es el dato que constantemente se repite, pero de igual modo encontramos que en la tabla se representan los datos entonces en conclusión la moda es el tipo de contrato indefinido y anual.

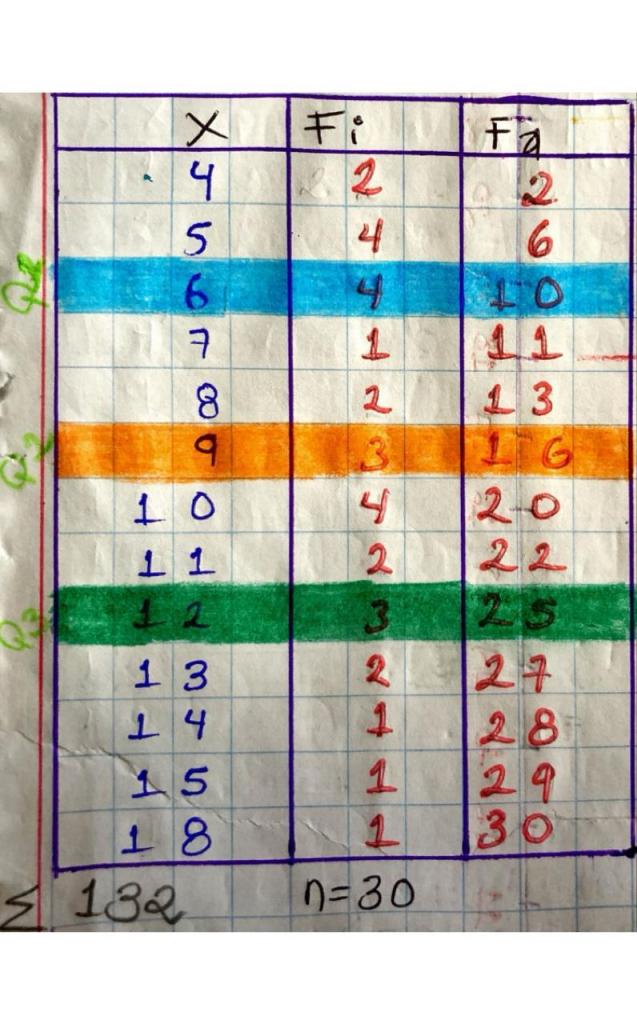
• Realiza un diagrama de tallo y hojas de la variable “Experiencia laboral” y al respecto es cribe una conclusión

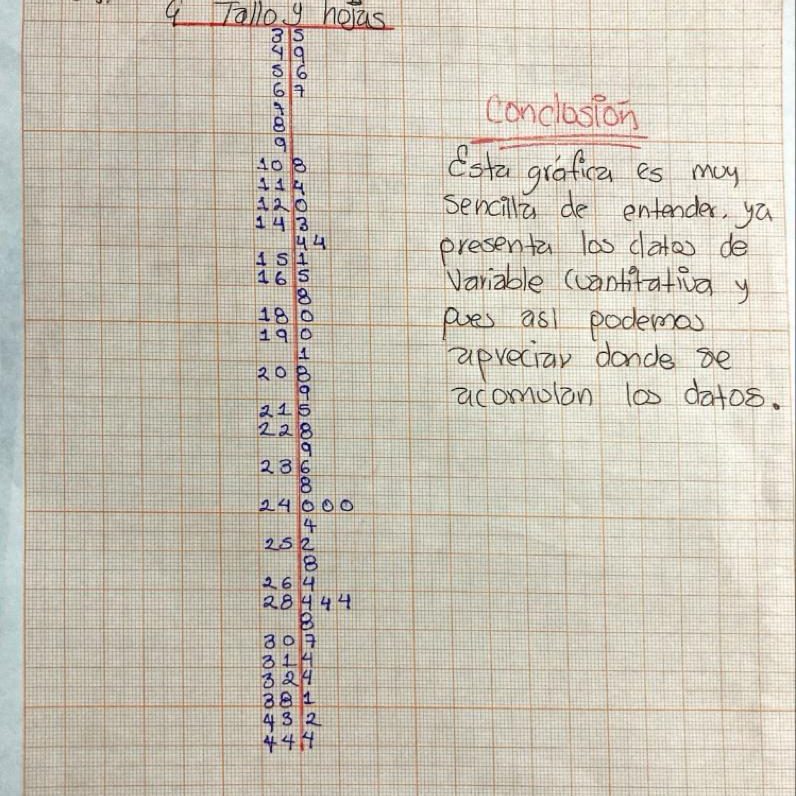
La distribución y representación de los datos en un diagrama de tallo y hojas es muy útil al ordenar variables cuantitativas, ya que podemos apreciar donde se acumulan los datos, variabilidad o dispersión y forma de distribución que tienen los datos, por este tipo de semi graficas conservan el valor de los datos.

EJERCICIOS: MTC Y MD DE DATOS NO AGRUPADOS

Instrucciones: resuelve los siguientes ejercicios, colocando el procedimiento y formulas empleadas para llegar a tu resultado.

1.- El gerente de la tienda Wal-Mart de la localidad estudia la cantidad de artículos que compran los consumidores en el horario de la tarde. A continuación, aparece la cantidad de artículos de una muestra de 30 consumidores.

15, 8, 6, 9, 9, 4, 18, 10, 10, 12, 12, 4, 7, 8, 12, 10, 10, 11, 9, 13, 5, 6, 11, 15, 5, 6, 6, 5, 13, 5.

1. Determine la media mediana y moda de los datos.
2. Obtenga el primer y tercer cuartil. Represente los datos en un diagrama de caja
3. Calcular, el rango, varianza, y desviación estándar.
4. Determina el C.V. y asimetría de datos.

Media: x= 4+4…18/30 = 273/30 = 91

Mediana: = 9+9/2=91

Moda: 5, 6, 10

Para poder obtener estos valores, se recomienda colocar los datos, de menor a mayor, para así sea más fácil de determinar lo que se nos pide.

Para calcular nuestros cuartiles, utilizamos la siguiente formula.

formula

Q= kn/4=k1   n=30

Definimos esta fórmula como la “posición” que es igual a k=1 multiplicado por el valor de nuestra frecuencia que es n=30 y posteriormente dividirlo entre 4.

Y así sucesivamente con nuestros dos cuartiles solo cambiamos la posición que en este caso era k=1 ahora es k=2 e igual con el Q3 k=3.

Nuestra segunda operación no es que algo sencillo, de hallar el rango intercuartílico RIQ y lo obtenemos de la siguiente forma

   

Q= kn/4=k1   n=30

Es buscar en nuestra tabla, el valor del Q3 y el Q1 estos dos valores se restan y así obtenemos nuestro RIQ.

Luego nos pide hallar el limite inferior y el límite superior.

De igual forma nos ubicamos en la tabla buscamos el valor de nuestro Q1 le restamos 1.5 y lo multiplicamos por el RIQ, para ello se realiza primero la multiplicación 1.5 por nuestro RIQ que en este caso equivale a 6, obteniendo este resultado, ya pasamos a realizar la resta y así obtenemos nuestro LI.

LI=Q1-1.5xRIQ

Para calcular nuestro límite superior, lo que realizamos es lo siguiente, ubicarnos nuevamente en la tabla, buscar nuestro Q3 que equivale a 12 mas 1.5 multiplicado por nuestro RIQ que es 6, ojos primero realizamos la multiplicación, 1.5 por 6 es igual a 9 posteriormente sumamos 12 + 9 nos da como resultado 21 y ese es nuestro LS.

LS=Q3+1.5XRIQ

    

Ya obtenido nuestros valores ahora si, a realizar nuestro diagrama de caja. Que no es mas que acomodar nuestros valores sobre una grafica recta, de acuerdo a tus datos de LI y LS, puedes hacerlo a escala, en donde posicionas, tanto como los dos limites, el dato menor y mayor y posteriormente los cuartiles.  Ya colocados los valores, trazar otra recta y sobre los Q1, Q2, Q3, realizar el diagrama, que no es mas que un rectángulo, para así, observar, en que lugar se posiciona más, nuestro dato.

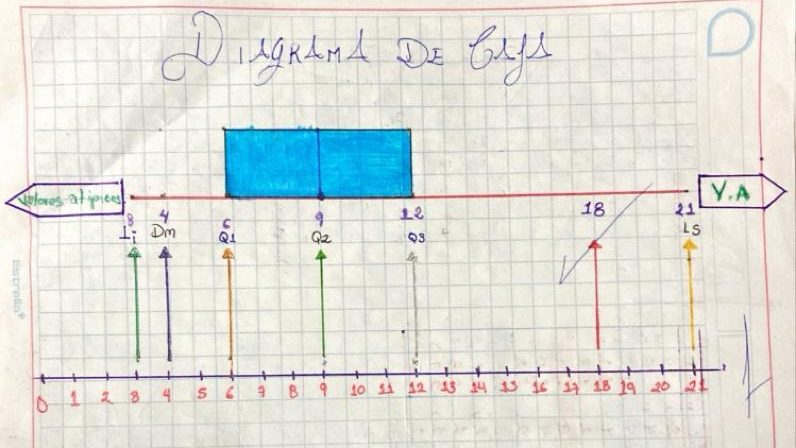
Posteriormente se nos pide calcular nuestro.

a) rango

b) varianza

c)desviación media y estándar

d)nuestro coeficiente de variación.

El rango es algo simple de calcular,

R= XMAX-XMIN

Nos posicionamos en nuestra primera tabla, que es nuestro dato mayor menos el dato menor, hacemos la resta y así obtenemos nuestro rango.

La varianza como sabemos nuestro primer dato es nuestra n=30 obtenida por la suma de nuestra frecuencia. 

Hacemos la respectiva operación y dividimos el resultado entre la frecuencia, pero se le resta -1 entonces así obtenemos el resultado.

En la desviación media, se recopila los datos de la tabla que aparece como (x1-M) y la colocamos en el siguiente cuadrante (1xL-M) todo con números positivos, ósea que había números negativos lo convertimos a positivo.

De igual forma nuestra desviación estándar es sacar la raíz cuadrada del resultado de nuestra varianza.

Coeficiente de variación es:
cv=desviación estándar/ Media

Solamente es colocar los datos obtenidos, y posterior en la división al final se hace la conversión a porcentaje. Y así obtenemos nuestro coeficiente de variación. 

En conclusión, la estadística es un proceso, que hace generalizaciones precisas sobre una población a partir de una muestra. Haciendo un énfasis, entre las dos (descriptiva e inferencial) se puede decir que es una ciencia que estudia datos, elementos, características en común. Para ser más explícitos, definimos que la:

• Población(N): es un conjunto de elementos que tiene una característica en común.
• Muestra(n): es una porción de la población.
• Variable: la definimos de este modo…
• Cualitativa: que son las cualidades
• Cuantitativa: esta se divide en dos, discreta y continua
• Discreta: Porque se expresa con números enteros
• Continua: se expresa con números con decimales.

Distribución binomial

La distribución binomial es un tipo de distribución de probabilidad discreta que describe la probabilidad de obtener un resultado específico en un número fijo de intentos o ensayos independientes. Este modelo es fundamental en estadística y teoría de la probabilidad, proporcionando un marco para comprender y predecir eventos en diversas áreas de estudio.

La probabilidad de cada posibilidad no puede ser más grande que 1 y no puede ser negativa.

las probabilidades se representan a continuación, del numero de probabilidades en este caso es 9, hacemos una combinación con la tecla de nuestra calculadora, que es indispensable en estos tipos de eventos estadísticos, combinamos nueve, posteriormente nos dará como resultado 1, luego multiplicamos al porcentaje que nos pide, en este caso es 90% elevándolo a la potencia 9, seguido multiplicamos 1- 0.90 y elevamos a la potencia 9 y así obtenemos nuestro primer resultado de nuestro ejercicio.

REFERENCIAS

Quevedo Ricardi, F. (s. f.). Estadística aplicada a la investigación en salud. Medwave. Recuperado 2 de marzo de 2011, de https://www.medwave.cl

Gonzalez Martinez, G. Estadística 1recopilacion de información. 24 febrero 2024.